Công thức tính khoảng cách giữa 2 mặt phẳng chuẩn nhất là gì?

Nhiều người thắc mắc Công thức tính khoảng cách giữa 2 mặt phẳng chuẩn nhất là gì? Bài viết hôm nay https://chiembaomothay.com/ sẽ giải đáp điều này.

Bài viết liên quan:

• Công thức tính nhiệt lượng chuẩn nhất
• Công thức tính khối lượng riêng chuẩn nhất
• Công thức tính lãi kép ngân hàng chuẩn nhất

Công thức tính khoảng cách giữa 2 mặt phẳng chuẩn nhất là gì?

Đôi nét về mặt phẳng:

Trong toán học, mặt phẳng là một mặt hai chiều phẳng kéo dài vô hạn. Một mặt phẳng là mô hình hai chiều tương tự như một điểm (không chiều), một đường thẳng (một chiều) và không gian ba chiều. Các mặt phẳng có thể xuất hiện như là không gian con của một không gian có chiều cao hơn, như là những bức tường của một căn phòng dài ra vô hạn, hoặc chúng có thể có quyền tồn tại độc lập, như trong các điều kiện của hình học Euclid.

Khi chỉ xét riêng trong không gian Euclide hai chiều, mặt phẳng đề cập đến toàn bộ không gian. Nhiều hoạt động cơ bản trong toán học, hình học, lượng giác, lý thuyết đồ thị và vẽ đồ thị được tiến hành trên không gian hai chiều, hay nói cách khác, trong mặt phẳng.

Công thức tính khoảng cách giữa 2 mặt phẳng chuẩn nhất là gì?

Trong mặt phẳng tọa độ không gian Oxyz, để xác định khoảng cách giữa 2 mặt phẳng ta phải biết được vị trí tương đối của nó. Ta biết, hai mặt phẳng (P) và (Q) có 3 vị trí tương đối có thể xảy ra:

Hai mặt phẳng trùng nhau
Hai mặt phẳng cắt nhau.
Hai mặt phẳng song song với nhau

Ta đã biết:

1. Hai mặt phẳng trùng nhau => Khoảng cách bằng 0: d = 0
2. Hai mặt phẳng cắt nhau=> Khoảng cách bằng 0: d = 0
3. Hai mặt phẳng song song với nhau có khoảng cách được bàn chi tiết trong bài này.

Khoảng cách giữa 2 mặt phẳng trong không gian được xác định như thế nào và được tính như thế nào, công thức ra sao ?. Tất cả các vấn đề trên sẽ được giải quyết trong bài viết này.

Cho hai mặt phẳng (P), (Q) song song trong không gian. Phương trình của chúng đều có thể đưa về dạng:
(P): ax+by+cz+d=0
(Q): ax+by+cz+d’=0 (a²+b²+c²>0 và d≠d’)

Khi đó giả sử M(α;β;γ) thuộc mặt phẳng (P) ta có: aα+bβ+cγ=-d. Khoảng cách giữa (P) và (Q) chính là khoảng cách giữa M và (Q). Do đó:

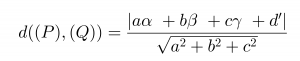
Vậy công thức tính khoảng cách giữa hai mặt phẳng song song là:

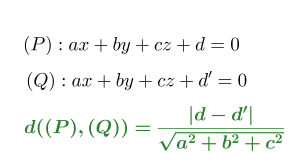
Ví dụ Công thức tính khoảng cách giữa 2 mặt phẳng

Bài tập 1. Trong không gian Oxyz, có hai mặt phẳng có phương trình lần lượt là (α): x – 2y + z + 1 = 0 và (β):  x – 2y + z + 3 = 0. Hãy tính khoảng cách giữa 2 mặt phẳng?

Hướng dẫn giải

Ta thấy hai mặt phẳng này song song với nhau nên khoảng cách giữa 2 mặt phẳng được xác định theo công thức

d((α); (β)) = |1–3|12+(–2)2√+12=6√3

Kết luận: d((α); (β)) = 6√3

Bài tập 2. Hai mặt phẳng (α) // (β), cách nhau 3. Biết phương trình của mỗi mặt phẳng là (α): 2x – 5y – 3z + 1 = 0 và (β):  ax + by + cz + d₂ = 0. Hãy xác định các hệ số của phương trình mặt phẳng (β).

Hướng dẫn giải

Vì (α) // (β) => a = 2; b = – 5 và c = – 3

Mặt khác: d((α); (β)) = 3 => |1–d1|22+(–5)2+(–3)2√=3⇔d1=338−−√–1

Kết luận: Phương trình mặt phẳng (β): 2x – 5y – 3z + (338−−√–1) = 0

Nguồn: https://toanhoc.org/

Qua bài viết Công thức tính khoảng cách giữa 2 mặt phẳng chuẩn nhất là gì? của chúng tôi có giúp ích được gì cho các bạn không, cảm ơn đã theo dõi bài viết.